流量計流量測量中常用的流體換算參數

對工業管道流體流動規律的研究、流量測量計算以及儀表選型時，都要遇到一系列反映流體屬性和流動狀態的物理參數．這些參數，常用的有流體的密度、粘度、絕熱指數(等熵指數)、體積壓縮系數以及雷諾數、流速比(馬赫數)等；這些物理參數都與溫度．壓力密切相關。流量測量的一次元件的設計以及二次儀表的校驗，都是在一定的壓力和溫度條件下進行的。若實際工況超過設計規定的范圍，即需作相應的修正。

一、流體的密度

流體的密度( 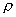 )是流體的重要參數之一，它表示單位體積內流體的質量。在一般工業生產中，流體通常可視為均勻流體，流體的密度可由其質量和體積之商求出：

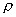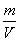 ＝                                   （1－2）

式中  m——流體的質量，kg；

      V——質量為m的流體所占的體積，m³

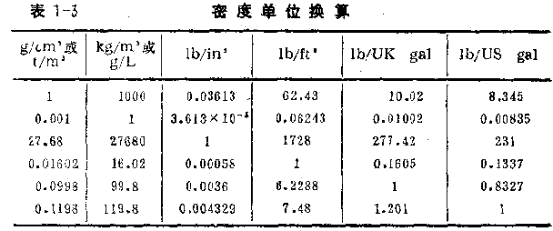
密度的單位換算見表1—3。

各種流體的密度都隨溫度、壓力改變而變化．在低壓及常溫下，壓力變化對液體密度的影響很小，所以工程計算上往往可將液體視為不可壓縮流體，即可不考慮壓力變化的影響．但這只是一種近似計算。而氣體，溫度、壓力變化對其密度的影響較大，所以表示氣體密度時，必須嚴格說明其所處的壓力、溫度狀況．

    工業測量中，有時還用“比容"這一參數。比容數是密度數的倒數，單位為m³／kg。

    二、流體的粘度

    流體的粘度是表示流體內摩擦力的一個參數。各種流體的粘度不同，表示流動時的阻力各異。粘度也是溫度、壓力的函數．一般說來，溫度上升，液體的粘度就下降，氣體的粘度則上升．在工程計算上液體的粘度，只需考慮溫度對它的影響，僅在壓力很高的情況下才需考慮壓力的影響。水蒸氣及氣體的粘度與壓力、溫度的關系十分密切．表征流體的粘度，通常采用動力粘度( 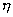 )和運動粘度(v)，有時也采用恩氏粘度(°E)．

流體動力粘度的意義是，當該流體的速度梯度等于l時，接觸液層間單位面積上的內摩擦力．流體的動力粘度也可理解為兩個相距1m、面積各為1m²的流體層以相對速度1m／s移動時相互間的作用力，即

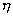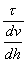        ＝                              （1－3）

式中 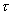   ――單位面積上的內摩擦力，Pa；

v——流體流動速度，m／s；

        h——兩流體層之間的距離，m；

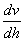         ——速度梯度，I / S；

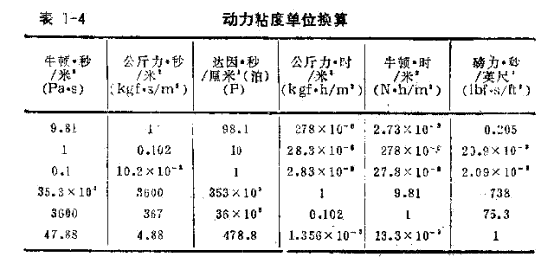
    動力粘度 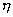 的單位Pa·s是單位制(SI)的導出單位，是我國法定單位．它與過去習慣使用的其他單位的換算關系見表l—4．表中  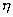的單位達因·秒／厘米²(dyn·s／cm²)是厘米—克—秒單位制(c．G．s單位制)的導出單位，習慣上稱泊(P)。取其百分之一為單位，稱厘泊(cP)，或百萬分之一為單位，稱微泊( 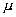P)。

由于流體的粘度和密度有關，將動力粘度與流體密度之比作為粘度的另一參數，稱運動粘度，用v表示：

           v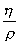＝                                        （1－4）

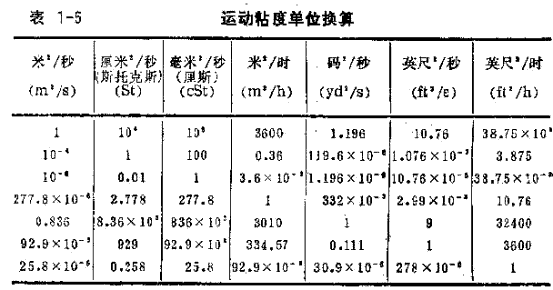
在SI單位制中，v的單位為m²/s與過去習慣用的其他單位間的換算關系見表1—5。表中v的單位cm²／s是c．G．s單位制的導出單位，稱斯托克斯(St)，取其百分之一為單位，稱厘斯(cSt)。

在試驗室對粘度進行測定常采用恩格勒粘度計，這里還需提及恩氏粘度(E)的概念。流體的恩氏粘度又稱條件粘度，它是基于流體的粘性越大，流動時表現的阻力也越大的原理,按下列方式測定的：取一定容積的被測流體(例如200mL)，在一定的溫度(t℃)下，測定其從恩格勒粘度計流出的時間( 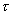t)，以s為單位，然后與同體積的蒸餾水在20℃時流出恩格勒粘度計的時間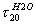（  ）對比，其比值稱該流體在t℃時的恩氏粘度．

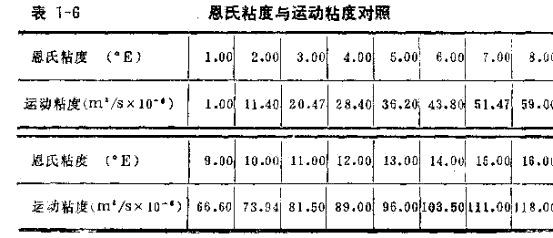
恩氏粘度與運動粘度在常用范圍內的對照關系見表1—6。當v＞1．2×l0^－4m²／s時，在同一溫度t下，E與v的換算采用下式：

             Et＝135×10³Vt                           （1－6）

或           Vt＝7. 41×10^－6Et                         （1－7）

式中   Et――在溫度t時的恩氏粘度；

Vt――在溫度t時的運動粘度。

三、牛頓流體及非牛頓流體

在節流裝置的設計標準、規程以及一些流量測量方法的“適用范圍"欄目中，常常提出所測流體于“牛頓流體"。什么是牛頓流體和非牛頓流體呢? 在前述流體的粘度一節中，給出了流體動力粘度的定義式(1—3)，由該式可以導出在流體內部有速度梯度(剪切進度) 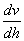時，作用在與該速度梯度方向垂直的單位面積上的內摩擦力(或稱剪切應力、粘滯力)  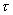與 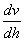 之間的關系式是：

式(1—8)稱牛頓粘性定律。當式中比例系數 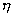 (即動力粘度)為常數時，內摩擦力  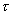與速度梯度 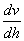 間呈線性關系。這一規律的流體即稱牛頓流體．不同種類的牛頓流體的比例常數  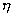值

各不相同。當 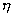 值不是常數或  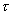與 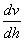 間的關系不符式(1—8)所示規律，即不符牛頓粘性定律時，該流體即稱非牛頓流體。一般高粘滯性流體和高分子溶液都呈現非牛頓流體的性質。典型的非牛頓流體以可塑性流體、膨脹性流體和賓厄姆(BINGham)流體為代表．其  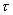與 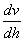 的關系可用下列兩個簡單的典型式表示：

當式(1—9)中常數n＞I時，稱可塑性流體；當n＜1時，稱膨脹性流體．對賓厄姆流體，表達式為

 式中 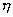    _B——常數，稱塑性粘度；

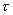 h——流體開始流動時的內摩接力(剪切應力)，常稱為屈服值。

為直觀起見，常以 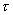 作縱坐標，以  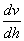為橫坐標，繪出  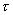與 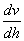 的關系曲線，稱流動曲線。對牛頓流體，流動曲線為通過原點的直線；對非牛頓流體，流動曲線有各種不同的形狀。例如可塑性流體的流動曲線是下彎的曲線；膨脹性流體則是向上彎的曲線；賓厄姆流體為不通過原點的直線。

    四、絕熱指數及等熵指數

    測量氣(汽)體流量時，需要了解流體流經流量測量元件(例如節流元件)時的狀態變化，為此需要知道被測氣(汽)體的絕熱指數和等熵指數。

    流動工質在狀態變化(由一種狀態轉變到另一種狀態)過程中若不與外界發生熱交換，則該過程稱為絕熱過程。若絕熱過程沒有(或不考慮)摩擦生熱，即為可逆絕熱過程．根據熵的定義，在可逆絕熱過程中熵(S)值不變(S＝常數)，故可逆的絕熱過程又稱為等熵過程。例如，流體流經節流元件時，因為節流元件很短，其與外界的熱交換及摩擦生熱均可忽略，所以該過程可近似認為是等熵的．在此過程中，流體的壓力P與比容V的X次方的乘積為常數，即PV^X＝常數，X稱為等熵指數。當被測氣(汽)體服從理想氣體定律時，等熵指數等于比熱比，即定壓比熱Cp與定容比熱Cv之比值Cp／Cv。在絕熱過程中，比熱比又叫絕熱指數。

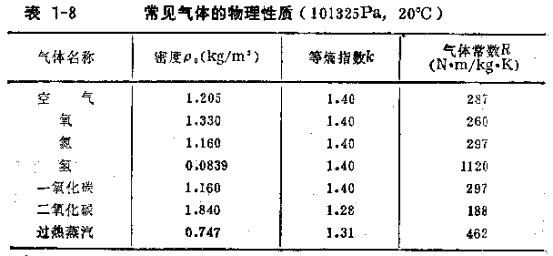
實際氣(汽)體的等熵指數與介質的種類以及所處的壓力、溫度有關，可從有關手冊的圖表上查取．幾種常用氣體在常溫常壓下的X值見表l—8。至今還有許多氣體或蒸汽的等熵指數尚沒有數據發表，在此情況下可暫時用比熱比代替。混合氣體的等熵指數不服從疊加規律，但其定壓比熱和定容比熱服從疊加規律，可按疊加法則求得，然后再求出混合氣體的比熱比．

    五、可壓縮流體的壓縮系數

任何流體都可壓縮，這是流體的基本屬性。但在工程上液體一般可忽略其體積的微小變化，視為不可壓縮^①。對于氣體，通常作為可壓縮流體來處理。在流量測量中，氣體流經測量元件的時間很短，來不及與外界進行熱交換，且可不考慮摩擦生熱，所以這時發生的氣體狀態變化過程可近似地視為可逆絕熱過程或等熵過程。因此，可用絕熱過程狀態方程來計算不同狀態下的比容(V)或密度( 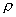 )．但由于PV^X＝常數這*熱方程的形式用來換算不同狀態下的比容或密度很不方便，在工程上仍用  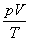＝mR(常數)這個理想氣體狀態方程式，只是再加一個實際氣體偏離理

想氣體的校正系數，這稱為壓縮系數(K₀)．此時，氣體狀態變化的基本關系式為

因為V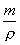＝  （m――氣體的質量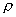；  ――氣體的密度），所以

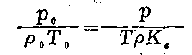
或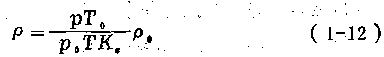             

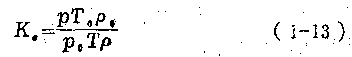
式中 P、T、V、 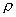 ——分別表示被測氣體的壓力(Pa)，溫度(K)，在P、T狀態下的容積(m³)和密度(kg／m³)；

P₀、T₀、V₀、 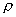₀——分別表示被測氣體在已知狀態時的參數，一般情況下取P₀＝1．0×l. 0 325×l0⁵  Pa，T₀＝273．15K。

由式(1—13)，壓縮系數K₀的物理意義就很明確，即根據理想氣體狀態方程求得的氣體容積和實際氣體間在各種壓力、溫度下有不同程度的偏離。壓縮系數就是衡量這種偏差程度的尺度。不同的氣體，壓縮系數也不同。各種氣體的壓縮系數可由有關工程手冊所載曲線查取，至于混合氣體的壓縮系數，可按下式確定：

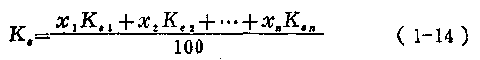
式中   X1，X2，…Xn——混合氣體各組成部分所占容積的百分比；

       K₀1，K₀2，…，K₀n——混合氣體各組成部分的壓縮系數。

K₀值確定后，即可代入式(1—12)，根據某一已知狀態下的密度 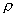 。值求出任一狀態下的密度  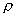．只有求出實際工作狀態下的密度  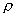，才能正確地求得該流體的流量．

—————————————————————

 ①壓力較高及測量準確度要求較高時，需考慮液體的可壓縮性。

六、馬赫數(流速比)

    流體的流動速度(V)和聲音在該流體內傳播的速度(c)之比，稱為馬赫數(M)，M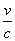＝  ．在氣體動力學中，它是劃分氣體流動類型的一個標準，又是判斷氣體壓縮性的一個尺度。

    在氣(汽)體中，壓力以聲速相對于氣體傳播．當氣(汽)體以流速V流動時，在順流情況下，壓力向下游傳播的速度是c+V；在逆流情況下，壓力向上游傳播的速度是c－V，因此，

當V＞c時，下游壓力的改變不會向上游傳播。音速噴嘴就是利用這一原理達到恒定酌臨界流量的。當馬赫數M＞l時，稱為超音速流動；M＜1時，稱為亞音速流動．在超音速和亞音速流功情況下，氣(汽)體表觀的特性有本質的區別。

流體的壓縮性是指機體在流場中相對密度的變化。實驗證明，隨著氣(汽)體流速增加，氣(汽)流中的壓力梯度也增加，則流體的密度就不能視為常數。因此，馬赫數就可用作衡量氣體壓縮性的標準。流體在流場中相對密度的變化( 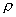 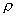／  。)和馬赫數是什么關系？工程上常遇到的等熵過程(例如氣體在噴嘴或葉片中的流動)的表達式為

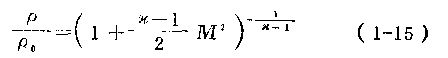
式中  X——等熵指數；

      M——馬赫數；

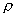 ——氣體在流動狀態下的密度；

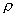0——氣體在滯止狀態(流速等于零)下的密度。

    由式(1—15)可知，氣體在流場中密度的變化是馬赫數的函數，并和氣體的性質有關．對于同一氣體，馬赫數越大，密度變化也就越大。例如，工業上常用的過熱蒸汽的 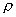 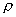／ 0和M的關系如表1—7所示。

由表1—7可知，隨著馬赫數的增加，也即隨著流速的增加，氣體的密度將減小。

在工業測量中，若馬赫數不大，則可利用式(I—15)計算得 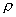 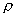／ 0，若在允許的誤差范圍內  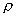的變化可忽略，則可根據具體情況把可壓縮流體視為不可壓縮流體處理。

音(聲)速和介質的性質以及所處的狀態有關，在工程上，聲速可用下式表示：

式中  X——介質的等熵指數；

      R——氣體常執，N·m／kg·K；

      T——工作狀態下介質的溫度，K。

在不同的氣體中音速各不相同。在0℃的空氣中音速為332m／s；在二氧化碳氣體中，為262m／s；在同一氣體中，音速隨溫度的升高而增加。應根據介質的性質以及工作狀態下的溫度由式(1—16)計算聲速。常見氣體的物理性質見表1—8所列。

七、雷諾數

測量管內流體流量時，往往必須了解其流動狀態、流速分布等。雷諾數就是表征流體流動特性的一個重要參數．

流體流動時的慣性力Fs和粘性力(內摩擦力)Fm之比稱為雷諾數。用符號Re表示。Re是一個無因次量。

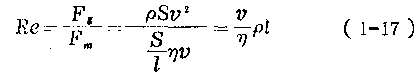
式(1—17)中的動力粘度 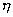 用運功粘度V來代替，因  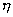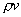＝  ，則

式中  V——流體的平均速度；

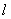       ——流束的定型尺寸；

      V、 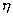 ­­——在工作狀態下流體的運動粘度和動力粘度；

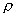 ——被測流體密度。

    由式(1—18)可知，雷諾數Re的大小取決于三個參數，即流體的速度、流束的定型尺寸以及工作狀態下的粘度。

用圓管傳輸流體，計算雷諾數時，定型尺寸一般取管道直徑(D)，則

用方形管傳輸流體，管道定型尺寸取當量直徑(Dd)。當量直徑等于水力半徑的四倍。對于任意截面形狀的管道，其水力半徑等于管道截面積與周長之比．所以長和寬分別為A和B的矩形管道，其當量直徑 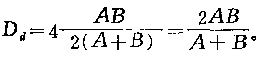對于任意截面形狀管道的當量直徑，都可按截面積的四倍和截面周長之比計算。因此，雷諾數的計算公式為

雷諾數小，意味著流體流動時各質點問的粘性力占主要地位，流體各質點平行于管路內壁有規則地流動，呈層流流動狀態。雷諾數大，意味著慣性力占主要地位，流體呈紊流流動狀態，一般管道雷諾數ReD＜2000為層流狀態，ReD＞4000為紊流狀態，ReD＝2000――4000為過渡狀態。在不同的流動狀態下，流體的運動規律．流速的分布等都是不同的，因而管道內流體的平均流速 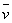 ；與zui大流速Vmax的比值也是不同的。因此雷諾數的大小決定了粘性流體的流動特性。圖1—l表示光滑管道的雷諾數ReD與  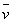／Vmax的關系。

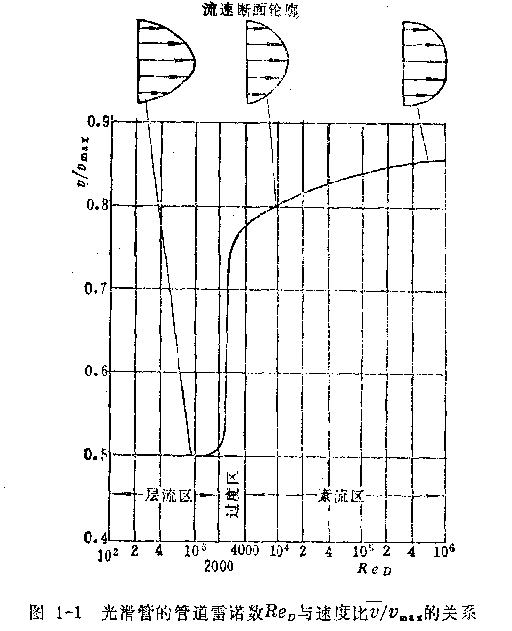
試驗表明，外部條件幾何相似時(幾何相似的管子，流體繞過幾何相似的物體等)，若它們的雷諾數相等，則流體流動狀態也是幾何相似的(流體動力學相似)。這一相似規律正是流量測量節流裝置標準化的基礎。可見，雷諾數確切地反映了流體的流動特性，是流量測量中常用的參數．

雷諾數的流量表達式為

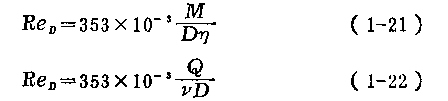
M——被測介質的質量流量，kg／h；

Q――被測介質的容積流量，m³／h；

D——管道內徑，mm；

 ——工作狀態下被測介質的動力粘度，Pa·s；

v——工作狀態下被測介質的運動粘度，m²／s。

    式(1—21)、  (1—22)中的常數值，依式中各參數的單位不同而異。當采用非式中的單位時，常數值應作相應的修正。

    在使用雷諾數時，應注意其對應的定型尺寸。一般在給出的雷諾數Re的右下角注以角碼，表明對應的定型尺寸。在節流裝置的標準中，對管道直徑D而言的雷諾數記作ReD，而對節流元件孔徑d而言的雷諾數記作Red，兩者的關系式為ReD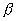＝  Red，式中  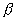為節流元件的直徑比，即  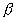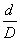＝  ．使用時應注意．