電化學阻抗譜(EIS)是分析復雜電化學系統的強有力工具。您可以瀏覽技術報告Basics of EIS,里面有對EIS的全面介紹。而那則技術報告中提及的大多數內容,本文將不再贅述。
本技術報告實際討論了EIS數據分析常見的方法,給大家甚至是初學者提供從EIS阻抗譜理解電解池中物理過程的基本方法。本文特意回避了與EIS數據分析相關的復雜數學計算。
使用EIS時,您在一個廣泛的交流頻率范圍內測試電解池的復阻抗。通常,系統的EIS阻抗譜由幾個電解池元件和電解池特征促成。一部分可能的元件包括:
電極雙電層電容
電極動力學
擴散層
溶液電阻
很遺憾,系統在任意給定頻率的阻抗通常依賴于多個電解池元件,這大大地增加了EIS阻抗譜的分析難度。
分析EIS阻抗譜常用的方法是等效電路模擬,也就是將上述所提元件合并后對電解池進行建模。每個元件的行為用“經典”電學元件(電阻,電容,電感)和一些專門的電化學元件(例如Warbug擴散元件)來描述。
過程的第一步是憑知識或經驗的猜測。您先預測覺得在電解池阻抗中起作用的系統元件。然后將這些元件建成一個等效電路模型。其中,將元件排列成邏輯的串并聯組合是擬合研究成功的關鍵。
在模型中的每一個元件都有一個已知的阻抗行為。元件的阻抗依賴于元件的類型和表征該元件的參數值。舉個例子,一個在頻率f被正弦波激發的電容器的阻抗可由下式表示:
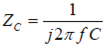 (1)
(1)
Zc是復阻抗,j是√-1,f是頻率(單位為赫茲),C是電容值(單位為法拉)。當用公式表示一個系統模型時,通常不知道系統中元件的參數值。舉個例子,知道涂漆金屬有一個涂層電容但并不知道這個電容的數值。
包含在Gamry公司EIS300 電化學阻抗軟件中的Echem Analyst Software軟件有一個圖形模型編輯器。您可以使用模型編輯器來形象化地建立一個等效電路模型。圖1顯示的是模型編輯器編輯的涂料模型,由EIS300提供。這個模型代表了金屬表面失效的漆膜的物理現象的一種可能的電路元件。關于該模型的具體表述,請瀏覽前面提及的EIS的初級報告。
您可以使用圖形模型編輯器來編輯相當復雜的電路。該方法的一個優點是您沒有必要像使用一些老舊的擬合程序似的去處理令人困惑的電路編碼。
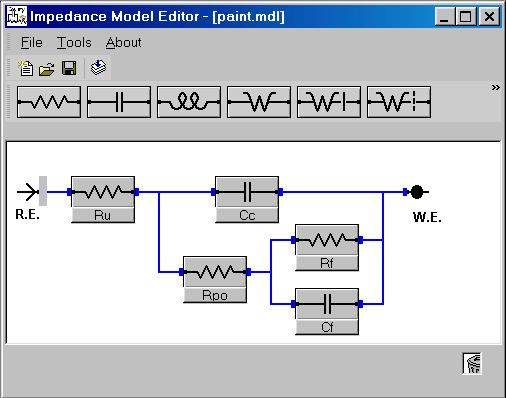
圖1 模型編輯器
該技術報告中的第二個例子涉及的是當模型預先無法知曉時,EIS擬合成模型的問題。在這之前,我們將先討論較簡單的已知模型的數據擬合案例。
一旦您覺得有一個模型代表了您的電化學系統,您使用非線性小二乘擬合程序去擬合實驗數據。這個程序嘗試將模型的阻抗譜和實驗數據阻抗譜間的誤差小化。
Echem Analyst里有兩種擬合算法—Levenberg-Marquardt算法和Simplex算法。兩種算法都會自動調整模型中元件的參數值以找到合適擬合值。擬合過程的數學細節不在該技術報告的討論范圍內。
等效電路擬合中一個比較困難的任務是確定模型參數的初始值。對于所有參數,兩種算法都需要從初始值(常被稱為種子值)開始。如果初始值與合適值相去甚遠,優化程序可能無法獲得合適擬合值。該技術報告的第一個例子論證了這一問題。
這個例子討論了當模型已知的的數據擬合。為了保證一個良好的擬合結果,數據用一個由電學元件組成的仿真電解池來記錄。各元件被分布在涂層模型中,如圖1所示。
圖2顯示的是Bode形式的原始EIS阻抗譜。因為Nyquist曲線中缺乏頻率信息比較難估算電容值,Gamry建議您用Bode曲線做擬合參數的初始估算。
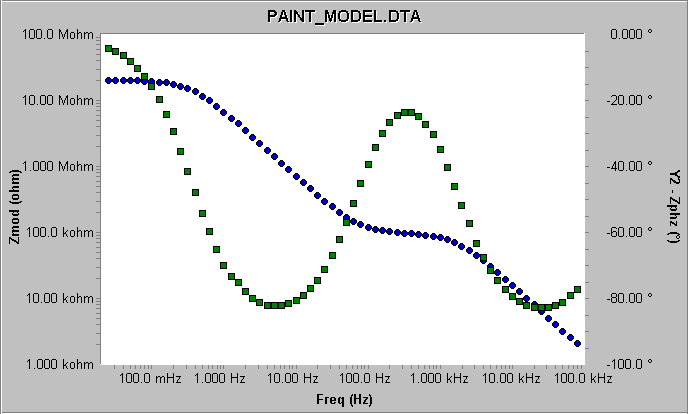
圖2 涂層模型仿真電解池的原始阻抗譜
如果您用該涂層模型擬合數據時,沒有調節參數的“初始值”(或按了Reset恢復到默認值),您可能會得到一個匹配錯誤的信息或者一個較差的擬合結果(圖3)。擬合結果的數值大小(藍色)和相位(綠色)都無法與數據較好地吻合。
這個錯誤是由不好的模型參數初始值造成的。Echem Analyst EIS分析中的擬合算法需要初始值在終值的一到兩個數量級范圍內才能正確地進行擬合。當初始值與合適值相去甚遠時導致的擬合不穩定不是EIS300*的現象。其他EIS模型擬合程序同樣需要初始值具有這樣的精確度。
所以,如何估算初始值呢?這需要一個計算器,還需要您對電路中元件的表現有一定的了解。基本上,我們會嘗試找到EIS曲線中模型阻抗由一種元件所控制的區域,然后計算在該頻率處元件的近似值。
測試圖1中的模型。請記住電容的阻抗在高頻時接近于0,在低頻時接近于無限大。低頻時,模型中電容的阻抗非常得高。Cc和Cf都與電阻并聯。當電容阻抗較高時,電阻阻抗是決定因素。在圖1中的低頻,阻抗大約是107歐姆,相位角接近于0º(表現為電阻)。這是Rμ,Rp和Rf的總和。假設Rf>Rp>Rμ,您可以估算Rf是107歐姆。至此,您就擁有了您的第一個初始值!
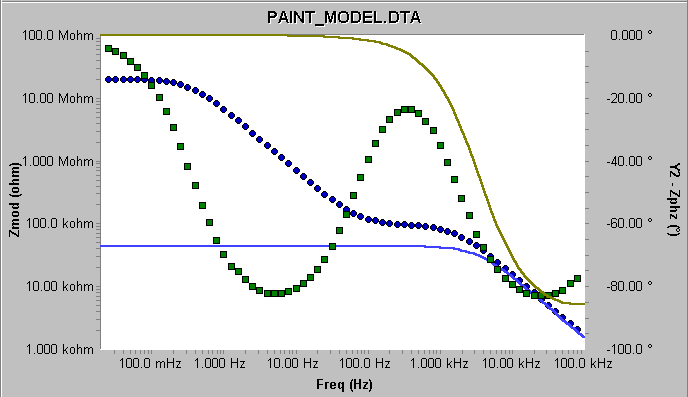
圖3 將所有初始值重置成默認值的擬合
1Hz以上的阻抗降起因于Cf。10Hz處,系統的阻抗大約是106歐姆。使用該值作為公式中電容的阻抗,忽略公式中的j,f=10Hz:
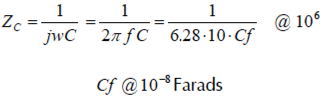
這是第二個初始值。
阻抗譜的中間區域,阻抗曲線趨近于一條水平線處看起來像另一個電阻。這肯定是Rp,我們可以給它賦一個大約為100 kΩ的值。
高頻區表現為電容性。10 kHz處的阻抗看似大約為10 kΩ。按照上述的程序走,但是104 Hz處的阻抗設為104歐姆,您就能獲得一個大約為10-9法拉電容值。這是Cc的初始值。
高頻數據永遠不會變為電阻式,這由阻抗的常數表明。Rμ必須比在高頻處使用的阻抗值要小。因此,用1歐姆作為初始值。
現在我們擁有了一組初始值,嘗試再來擬合一下。在參數窗口填入初始值。您可以用E的格式輸入電容值,例如1E-9表示10-9。按下Preview按鈕。您會看到一個與圖4類似的曲線。
需要注意的是種子曲線和實驗數據得到的阻抗值和相位角曲線的形狀相似。一般而言,每當這些曲線形狀相似而且初始值與合適值在100倍的范圍內時,模型將能擬合。
當按下Calculate,您可以看到擬合真的非常得好(圖5)。表1顯示了由擬合器計算所得的參數值,與仿真電解池各元件數值的比較。Levenberg-Marquadt和Simplex算法都給出了相同的結果。
Element | Fit Value | Component Value | ||
Rf | 20.12 E± 0.17 | Mohm | 20 | MΩ |
Cf | 21.55 E± 0.14 | nF | 22 | nF |
Rp | 100.4 E±0.9 | kohm | 100 | kohm |
Cc | 996. E± 7 | pF | 1000 | pF |
Ru | 418. E± 30 | ohm | 402 | Ω |
表1 擬合值和元件值
需要注意的是Rμ擬合值存在著很大的不確定性,并且真實Rμ值和擬合值之間符合得比較不好。這很容易解釋。我們說過,阻抗曲線永遠不會在高頻處變成電阻式。事實上,在高頻處的輕微幅角變化僅僅表示了Rμ的存在。一條重要的原則是:如果一個元件的阻抗在擬合頻率范圍內不是電解池阻抗的重要影響因素,該元件的參數值將會不好而且數值的不確定性會比較大。
兩種算法都顯示了一個“擬合優良度”的值。0.0001(1E-4)這個值表明是非常好的擬合結果,測得阻抗和計算值間僅有大約1%的差異。0.01被視為一個“一般”的擬合結果。差的擬合結果給出的是一個高于或等于0.1的值(30%測試誤差)。當不合適的模型被選擇時會得到這樣的結果,與實驗數據符合得不好。您應該另外探索一下其他的假說和模型以解釋您的數據。
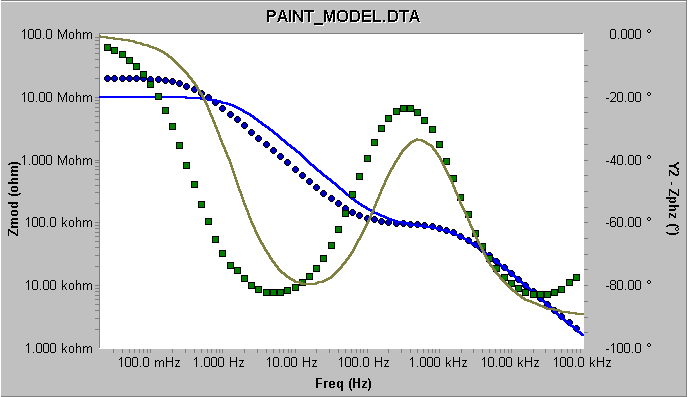
圖4 初始值—涂層模型
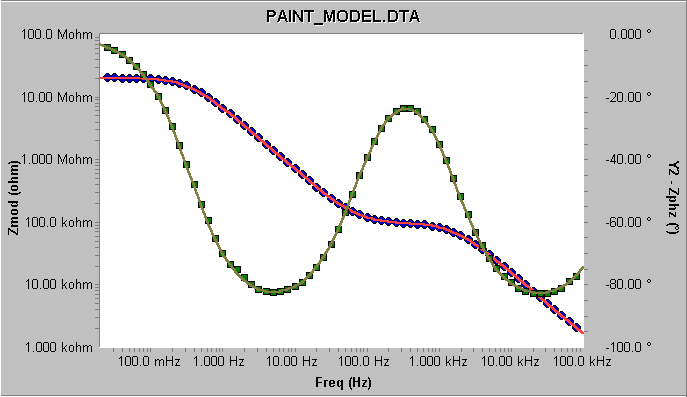
圖5 終擬合結果—涂層模型
在這個例子中,開始EIS數據分析前模型還是未知的。樣品是一個商業AA可再充堿性電池。在每一個充放電循環后,阻抗譜由Gamry混合EIS模式記錄。充電態的EIS阻抗譜比放電態的更加有趣,所以其中一個充電態阻抗譜被選作說明。
第一周充電循環后的阻抗譜如圖6(Bode曲線)和圖7(Nyquist曲線)所示。Bode曲線展示了與之前例子非常不同的行為,所以它被轉換成線性阻抗值以代替更常見的對數值。當頻率變化超過3個數量級時,阻抗值的變化小于30%!在對數范圍呈現的較小的變化非常令人困惑,所以線性比例被采用。幅角的變化也非常得小—幅角變化小于5º。
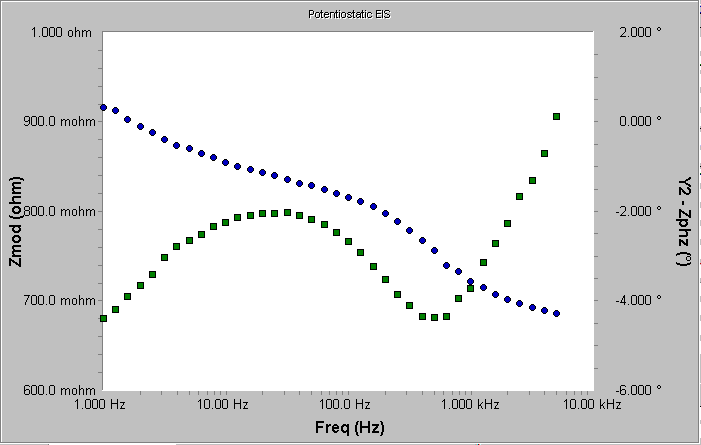
圖6 充電態電池的Bode曲線
Nyquist曲線(圖7)顯示了一個扁半圓,是Randels元件的典型特征。在低頻時,曲線顯示了一個完整的對角線,與水平線呈45º角,表明是Warburg阻抗。
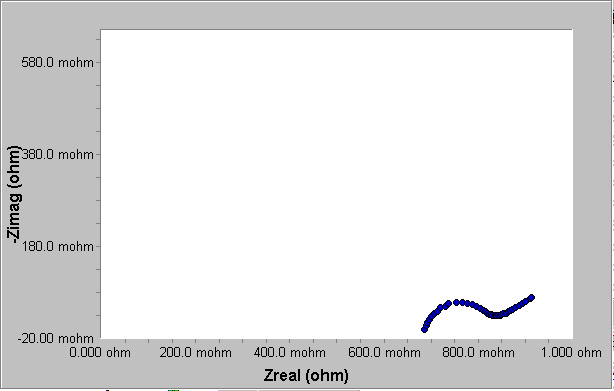
圖7 充電電池的Nyquist曲線
什么是該系統模型較好的起始點呢?
我們知道樣品是一個用兩電極模式測試的電池,所以它擁有兩個電極/電解質界面。
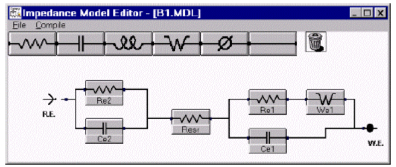
圖8 第一個切入模型—電池數據
我們可以假設每一個界面有一個雙電層電容和一個電荷轉移電阻。讓我們將Warburg阻抗給一個界面。
我們也知道電極間的溶液通道也有一個電阻。這是電池的等效串聯電阻(esr)。將這些事實和假設代入模型中,我們會得到如圖8所示的圖解。
再一次,在擬合曲線收斂(一個數學術語表示將得到一個好的擬合結果)前我們需要初始值。看看模型(并暫時忽略Warburg阻抗),高頻的極限阻抗是Resr。測試Bode曲線,您會看到在高頻處的阻抗大約是0.7 歐姆。使用這個值作為Resr的初始值。
低頻阻抗(10 Hz)大約是0.85 Ω。仍舊忽略Warburg阻抗,這個值是R1,R2和Resr的總和。由于我們估算Resr是0.7 Ω,所以R1加R2應為0.15 Ω。我們沒有好的方法可以把這兩個電阻的貢獻分開,因此我們將每一個的初始值設為0.075 Ω。
我們也不能夠表面地區分C1和C2的貢獻。在6000Hz到100Hz之間,電解池的阻抗變化了0.15Ω,將“中點”1000Hz代入上述電容阻抗方程式中。串聯的C1和C2的數值是1mF。串聯的電容與并聯的電阻相似,所以我們能夠給C1和C2分別賦一個初始值為2mF。
當您預覽使用這些值并給Warburg系數賦值1.0得到的種子曲線時,您會得到如圖9所示的曲線。
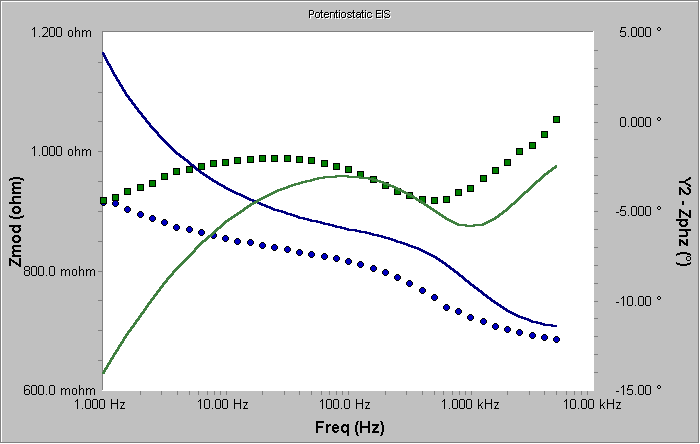
圖9 初始曲線的預覽—粗略估算
阻抗與相位角曲線都看起來與數據曲線的形狀相似,所以如果我們點選了Calculate按鈕時,我們就是安全的。
如果我們想要提高初始值,我們應當注意到Warburg元件導致了低頻阻抗的增加。降低Warburg系數將會使這個增加在任何給定頻率下變小。圖10顯示了Warburg系數增加到3的初始值曲線。
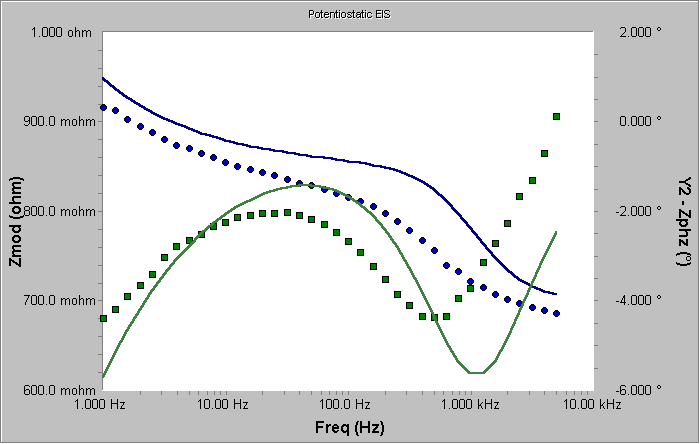
圖10 Warburg系數為3的初始曲線
使用任意一組初始值,選擇Calculate將得到圖11中的曲線
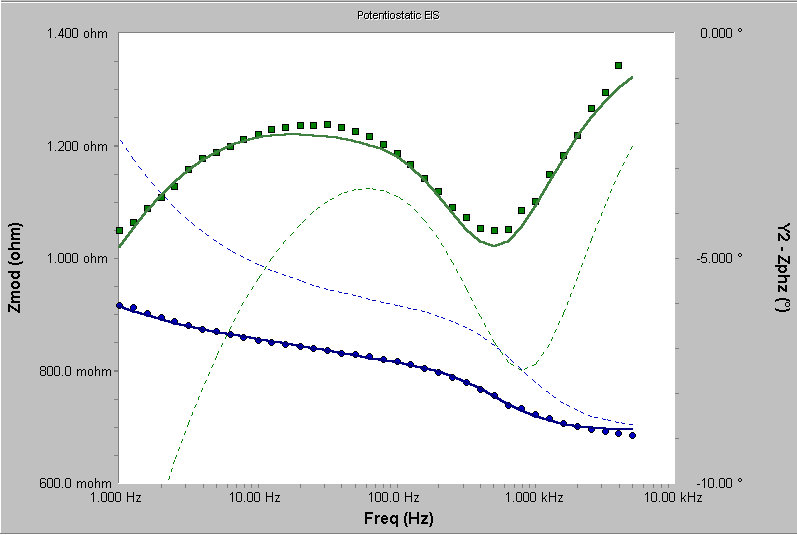
圖11 與初始模型進行擬合
擬合結果不太糟,但是有一些明顯的誤差,尤其是相位角。讓我們嘗試用恒定相元件(CPE)替代兩個電容。新的模型如圖12所示。
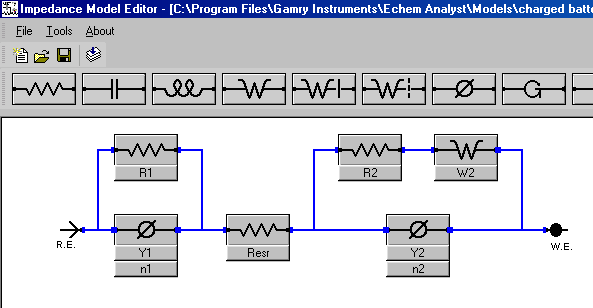
圖12 使用CPE的電池模型
我們可以使用前述擬合中尋得的數值來計算新的CPE元件的初始值。前面的擬合數值可以在圖11中的表格中查看。請記得第一個CPE參數與電容值相等。因此,Y2的初始值是0.075,Y1的初始值是0.0027。使用1.0作為兩個CPE參數α的初始值。
當我們輸入這些新的初始值到新的模型中,然后按Calculate按鈕,我們可以得到曲線如圖13所示。
圖13 第二切模型擬合
仔細比較圖11和圖13可以發現,CPE元件略微提高了10Hz到100Hz間的幅角擬合。這個提高可能不夠大以證明CPE和它任意參數α的存在。如果我們來看看每一個模型的“擬合優秀”的數值,我們可以把它稍微量化一下。數值都列于下表中擬合結果的后一行。
Capacitor Model | CPE Model |
表2 比較兩種電路模型擬合的優良度
兩種模型的“擬合優良度”都非常好:兩個的值都在1e-4的標準以下,表示擬合良好。不過,兩個的數值幾乎相等:他們僅相差大約10%。根據經驗,如果“擬合優良度”的數值相差少于3個數量級,那兩個模型可以被視為“無法區分”。CPE模型應該僅在它的“擬合優良度”數值低于12e-6或(37e-6)/3時才會被考慮。
需要注意的是,當僅有兩端EIS測量可用時,我們無法區分電池的負極和正極界面。如果參比電極可以放入電解池,單獨界面的阻抗可以被測量。
用EIS模型擬合實驗數據是一個非常簡單的工作。它僅需要您對您所測電解池及其原理稍微有點兒了解,然后對電解池元件的表現行為有一個基本的認識。
如果您沒有一個現成的模型,那就從檢測數據開始。尋找相位角中的谷值,它反映的是數據中的拐點。使用您對電解池的了解,參考實驗數據提出一個模型。在很多例子中,EIS300提供的標準模型可以提供一個終模型或者一個可以發展您自己的模型的好的起始點。
Gamry不建議您向模型中增加元件直到擬合中所有的可視誤差都消除了。模型中如果包含在電解池化學過程中沒有任何基礎的元件時會得到一個很好的擬合結果,不過這個結果不能夠提供關于電解池行為的任何實用信息。
一旦您建立起一個模型,首先估算電阻值。尋找Bode曲線中的水平區域,然后將它們賦成單個的或者串聯的電阻。然后按文中的方法估算電容的數值。在您做這些估算時,沒必要太精確。任何與真實數值在1個數量級差別以內的數值都是好的起始點。
后,使用預覽特征來檢查您的估算。此時,您可以微調模型中Warburg阻抗的初始值。一般而言,每當初始曲線與數據曲線的形狀相似時,擬合算法將會收斂。如果兩者曲線擁有不懂的形狀,擬合程序可能失敗。
后,執行擬合,檢查結果。如果擬合結果看起來不太好,您可能需要調整模型,重復上述過程。
要下載本應用報告的PDF文件嗎?
First Name:
Surname:
Email address:
立即詢價
您提交后,專屬客服將第一時間為您服務